300. 最长递增子序列

YiSen

2023-07-26

leetcode

Vue3 diff, 二分查找, 动态规划, 最长递增子序列, 贪心算法

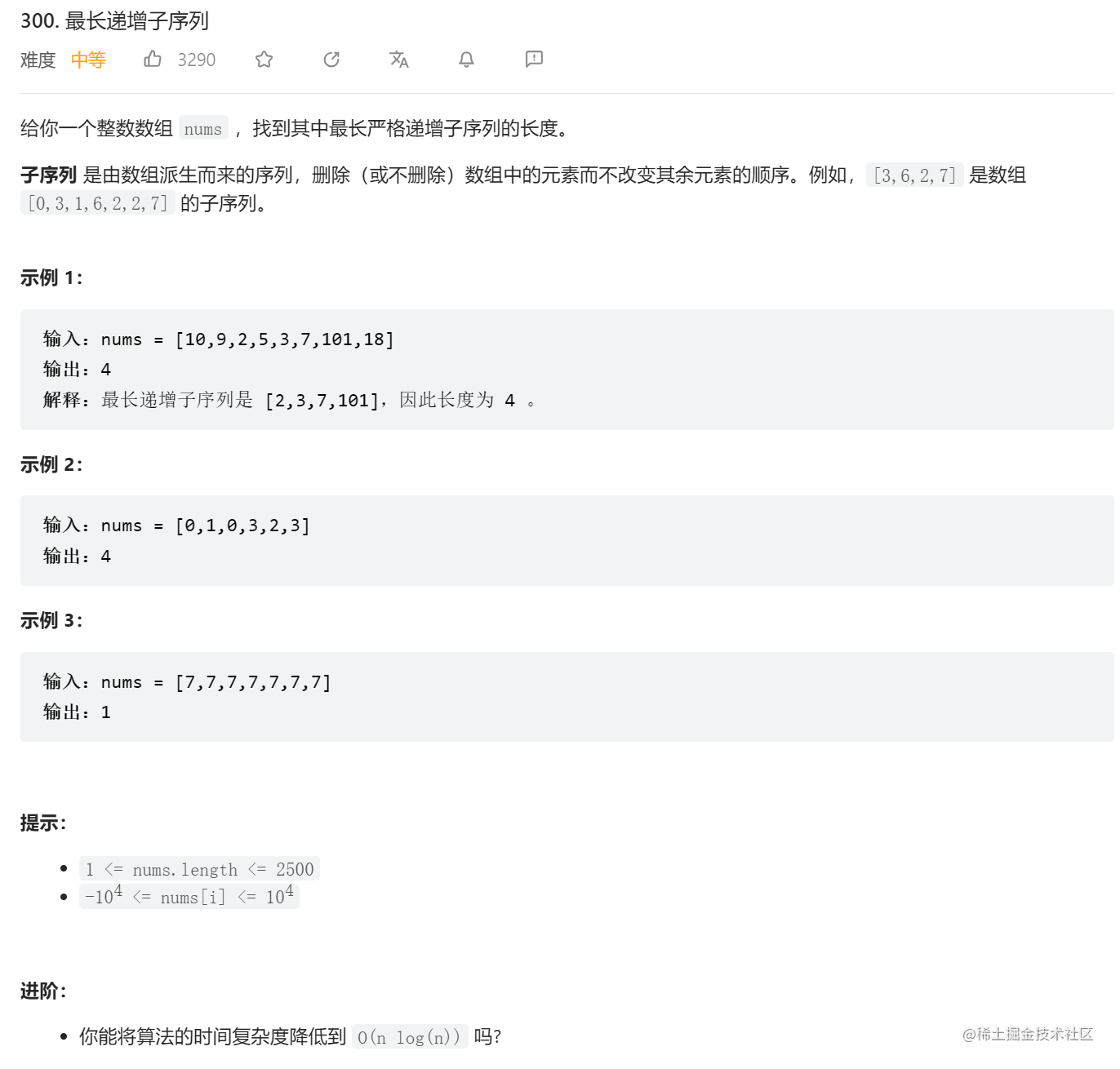
题目

特殊情况

长度为0或1的序列，最长子序列长度也只可能为0或1

思路一动态规划

dp：从第一个元素到第i个元素的最长递增子序列长度是固定的，第一个元素的最长递增子序列长度为1。

编码

/**
 * @param {number[]} nums
 * @return {number}
 */
var lengthOfLIS = function (nums) {
  // 特殊情况
  if (nums.length <= 1) return nums.length;
  // dp
  let dp = Array.from({ length: nums.length }).fill(0);
  // 第一个元素的最长递增子序列长度为1。
  dp[0] = 1;
  // 目前最长递增子序列长度
  let maxLen = 1;
  // 遍历
  for (let i = 1; i < nums.length; i++) {
    let maxDp = 0;
    // 找到符合递增的最长子序列长度
    for (let j = 0; j < i; j++) {
      if (nums[j] < nums[i]) {
        if (dp[j] > maxDp) maxDp = dp[j];
      }
    }
    dp[i] = maxDp + 1;
    // 找出最长的递增子序列长度
    if (dp[i] > maxLen) maxLen = dp[i];
  }
  return maxLen;
};

复杂度

时间复杂度：O(n^2)

空间复杂度：O(n)

思路二贪心 + 二分查找

贪心：前面的元素越小，后面可放置的元素可能就越多（这题只需要求长度，最长递增子序列的正确性不考虑）

编码

 * @param {number[]} nums
 * @return {number}
 */
var lengthOfLIS = function (nums) {
  if (nums.length <= 1) return nums.length;
  let ansArr = [nums[0]];
  for (let i = 1; i < nums.length; i++) {
    let val = nums[i]
    let lastEl = ansArr[ansArr.length - 1]
    // 大于最大元素直接push
    if (val > lastEl) {
      ansArr.push(nums[i])
    } 
    // 等于最大元素略过
    else if (val === lastEl) {
      continue
    } 
    // 小于最大元素进行二分查找
    else if (val < lastEl) {
      let l = 0, r = ansArr.length - 1
      while (l < r) {
        let mid = l + ((r - l) >> 1);
        if (ansArr[mid] >= val) {
          r = mid
        } else {
          l = mid + 1
        }
      }
      ansArr[l] = val
    }
  }
  return ansArr.length;
};

复杂度

时间复杂度：得益于二分查找，时间复杂度为O(nlogn)。

空间复杂度：O(n)

扩展：贪心加二分查找怎么求最长子序列

这个在LeetCode上找不到有对应的题，有知道的大佬也请留言告知一下。

想这个是从vue3得到启发的，毕竟如果解决不了实际问题就不会有人去钻研算法了，最长递增子序列如果只知道个长度，那么能解决的问题就很少了，然而vue3中的DOM DIFF刚好就利用了这个，那么就来看看vue3是如何解决的吧。

源码在这

core/packages/runtime-core/src/renderer.ts at 3be4e3cbe34b394096210897c1be8deeb6d748d8 · vuejs/core (github.com)

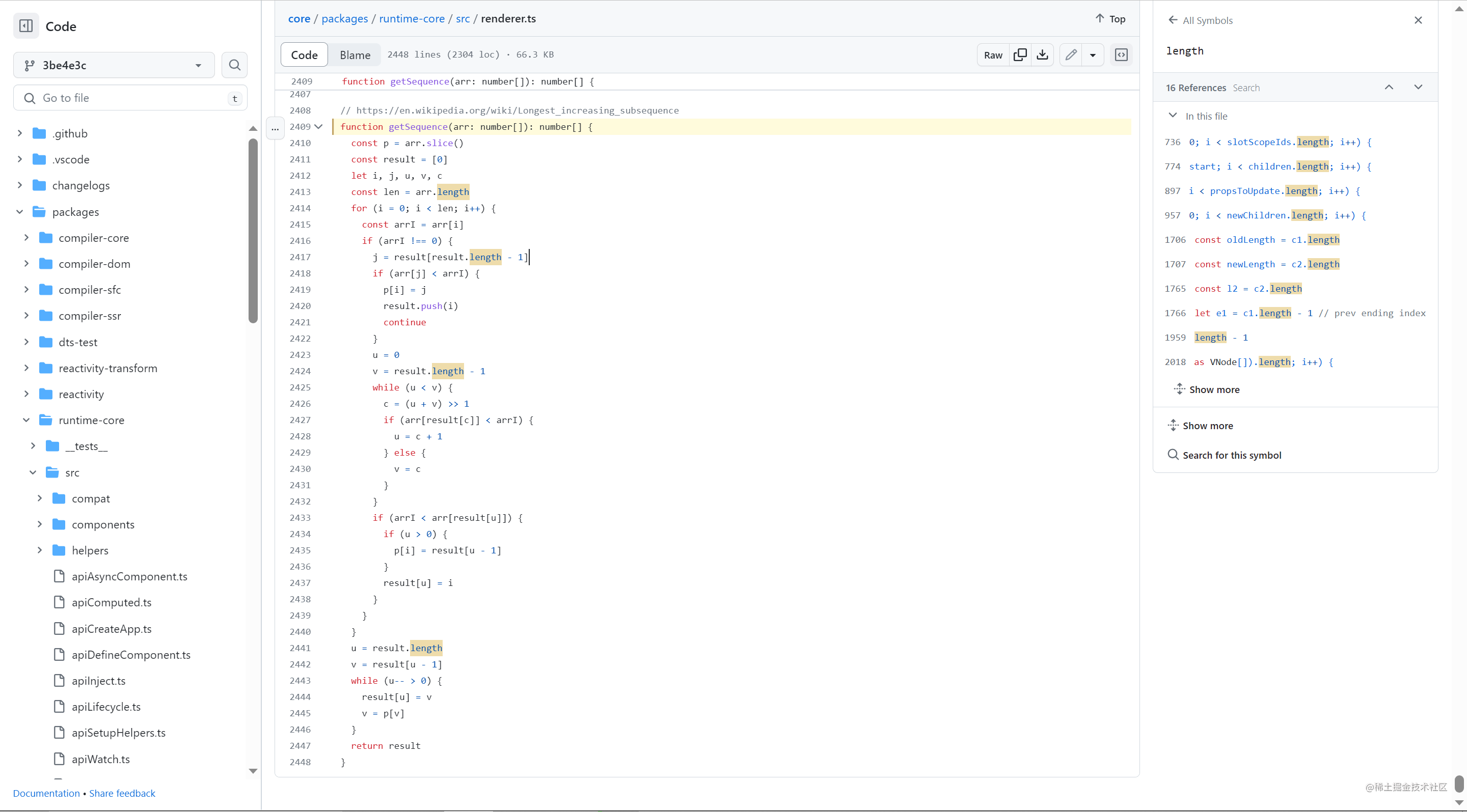
思路解析

在原本贪心加二分查找的思路上，我们能得到一个序列a，假设最长递增子序列为b，可以确定的是：

a.length===b.length
a[a.length-1]===b[b.length-1]。

比如说：

[1,2,10,20,30,3,4]，根据贪心的思路，最终会得到a=[1,2,3,4,30]，而最长递增子序列为b=[1,2,10,20,30]。
[1,2,10,20,30,3,4,5]，根据贪心的思路，最终会得到a=[1,2,3,4,5]，而最长递增子序列为b=[1,2,10,20,30]/[1,2,3,4,5]。
[1,2,10,20,30,3,4,5,6]，根据贪心的思路，最终会得到a=[1,2,3,4,5,6]，而最长递增子序列为b=[1,2,3,4,5,6]。

根据以上的例子发现，贪心的过程基本都是会覆盖原本序列之前的元素，其中情况一中，覆盖后的序列不如原本序列长，则得出的序列并不是子序列，但符合长度相等和最后一项相同的特点。反之，情况二三就是要得到最终的最长递增子序列。

针对情况一，vue3添加了一个回溯的过程用于恢复原来被覆盖的元素。由于最后一个元素是一定是正确的，那么在贪心的过程中，我们记录上每个元素的前一个元素的下标，然后在回溯的过程中通过下标找回原本被覆盖的元素，即可得出正确的最长递增子序列。

举例

比如情况一中nums=[1,2,10,20,30,3,4]，在得到res=[1,2,10,20,30]之后，同时记录idxRes=[0,1,2,3,4]，recalls=[-1,0,1,2,3]。

recalls中除了第0项的-1，其余的元素都是相同下标的res[i-1]在原数组中的下标，比如i=4，res[i-1]==20,nums[recalls[idxRes[i]]]==20。

让我们继续贪心：res=[1,2,3,4,30]，idxRes=[0,1,5,6,4]，recalls=[-1,0,1,2,3,1,5]。其中res和idxRes都是覆盖，而recalls则是继续添加，其中在res中3覆盖10之后，前面的2在nums的下标为1，所以recalls中就多了一个1；同理4覆盖20的时候，前面是3，在nums的下标为5，所以recalls中就多了一个5。

到这里，若i=4，res[i-1]==4,nums[recalls[idxRes[i]]]==20。可以看到这里原本被4覆盖了的20又被找回来的。

基于这样的一个步骤一直回溯就能够得到最终的最长递增子序列。

编码

/**
 * @param {number[]} nums
 * @return {number[]}
 */
function LIS(nums) {
  // 记录回溯下标
  let recalls = [undefined];

  // 记录最新贪心序列以及对应下标
  let res = [nums[0]];
  let idxRes = [0];


  for (let i = 1; i < nums.length; i++) {
    // 大于push
    if (nums[i] > res[res.length - 1]) {
      recalls.push(idxRes[idxRes.length - 1])
      res.push(nums[i])
      idxRes.push(i)
    }
    // 等于略过
    else if (nums[i] == res[res.length - 1]) {
      continue
    }
    // 小于找位置插入
    else {
      // 查找
      let l = 0, r = res.length - 1;
      while (l < r) {
        let mid = (l + r) >> 1;
        if (res[mid] >= nums[i]) {
          r = mid
        } else {
          l = mid + 1
        }
      }

      recalls.push(idxRes[l - 1])
      res[l] = nums[i]
      idxRes[l] = i
    }
  }

  // 回溯
  for (let i = res.length - 1; i > 0; i--) {
    res[i - 1] = nums[recalls[idxRes[i]]]
    idxRes[i - 1] = recalls[idxRes[i]]
  }
  return res;
}

复杂度

时间复杂度：得益于二分查找，时间复杂度为O(nlogn)。虽然多了个回溯过程，但系数为1可省略。

空间复杂度：O(n)。同样是多了几个数组进行记录，但始终是常数个，最终还是与nums的长度相关。

题目